关于【抛物线的基本知识点】，抛物线的基本知识点有哪些，今天涌涌小编给您分享一下，如果对您有所帮助别忘了关注本站哦。

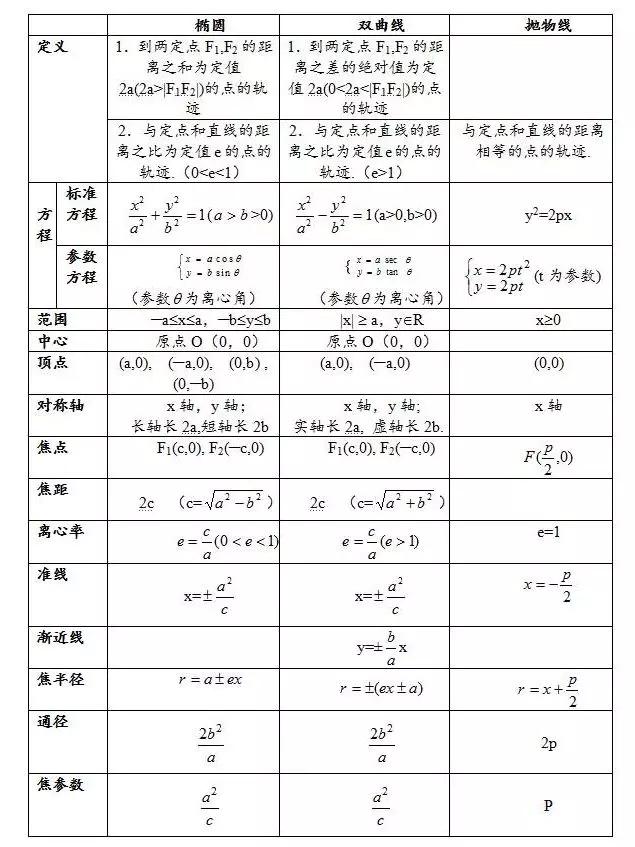
1、高中数学椭圆、双曲线、抛物线的重点知识归纳和常用结论汇总

双曲线

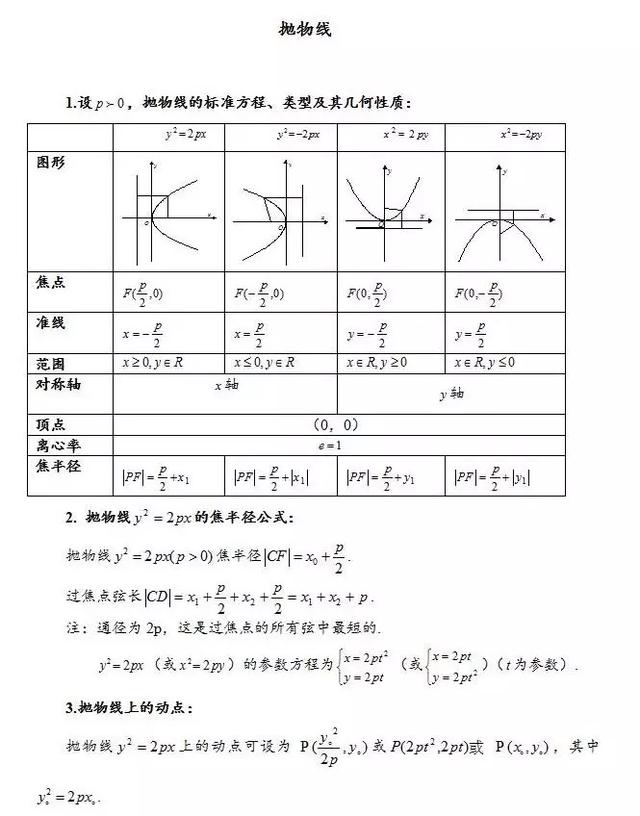
抛物线

圆锥曲线的综合问题

椭圆方程的第一定义

椭圆及其标准方程

椭圆的简单几何性质

2、抛物线的基本知识点有哪些

抛物线的基本知识点有哪些？

抛物线的基本知识点如下：
1.抛物线是轴对称图形对称轴为直线x=—b/2a，对称轴与抛物线唯一的交点为抛物线的顶点P，特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）。
2.抛物线有一个顶点P坐标为：P（—b/2a，（4ac—b^2）／4a）当—b/2a=0时，P在y轴上；当＝b^2—4ac=0时，P在x轴上。

4.一次项系数b和二次项系数a共同决定对称轴的位置当a与b同号时（即ab0），对称轴在y轴左；当a与b异号时（即ab0），对称轴在y轴右。
5.常数项c决定抛物线与y轴交点抛物线与y轴交于（0，c）。
6.抛物线与x轴交点个数＝b^2—4ac0时，抛物线与x轴有2个交点。＝b^2—4ac=0时，抛物线与x轴有1个交点。

＝b^2—4ac0时，抛物线与x轴没有交点。X的取值是虚数（x=—bb^2—4ac的值的相反数，乘上虚数i，整个式子除以2a）。

抛物线的知识点有哪些？

1.准线、焦点：抛物线是平面内到一定点和到一条不过此点的定直线的距离相等的点的轨迹。这一定点叫做抛物线的焦点，定直线叫做抛物线的准线。

3.弦：抛物线的弦是连接抛物线上任意两点的线段。
4.焦弦：抛物线的焦弦是经过抛物线焦点的弦。
5.正焦弦：抛物线的正焦弦是垂直于轴的焦弦。
6.直径：抛物线的直径是抛物线一组平行弦中点的轨迹。

这条直径也叫这组平行弦的共轭直径。
7.主要直径：抛物线的主要直径是抛物线的轴。
8.离心率：e=1（恒为定值，为抛物线上一点与准线的距离以及该点与焦点的距离比）
9.焦点：（p/2，0）
10.准线方程l：x=-p/21
1.顶点：（0，0）1
2.通径：2P ；定义：圆锥曲线（除圆外）中，过焦点并垂直于轴的弦。

1
3.定义域：对于抛物线y1=2px，p>0时，定义域为x≥0，p<0时，定义域为x≤0；对于抛物线x1=2py，定义域为R。1
4.值域：对于抛物线y1=2px，值域为R，对于抛物线x1=2py，p>0时，值域为y≥0，p<0时，值域为y≤0。扩展资料：有关切线、法线的几何性质（1）设抛物线上一点P的切线与准线相交于Q，F是抛物线的焦点，则PF⊥QF。

且过P作PA垂直于准线，垂足为A，那么PQ平分∠APF。（2）过抛物线上一点P作准线的垂线PA，则∠APF的平分线与抛物线切于P。〈为性质（1）第二部分的逆定理〉从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。

（3）设抛物线上一点P的切线与法线分别交轴于A、B，则F为AB中点。（4）设抛物线上除顶点外的点P的切线交轴于A，交顶点O的切线于B，则FB垂直平分PA，且FB与准线的交点M恰好是P在准线上的射影（即PM垂直于准线）。（5）抛物线的三条切线所围成的三角形，其外接圆经过焦点。即：若AB、AC、BC都是抛物线的切线，则ABCF四点共圆。

（6）过抛物线外一点P作抛物线的两条切线，连接切点的弦与轴相交于A。又设P在轴上的射影为B，则O是AB中点。（7）若抛物线与一个三角形的三条边（所在直线）都相切，则准线通过该三角形的垂心。

高中数学抛物线的基本知识点有哪些？

高中数学抛物线的基本知识点如下：
1.定系数法：根据条件设出标准方程，再确定参数p的值，这里要注意抛物线标准方程有四种形式。从简单化角度出发，焦点在x轴的，设为y2＝ax(a≠0)，焦点在y轴的，设为x2＝by(b≠0)。

3.由于抛物线的焦点可在任意半轴，故共有标准方程y^2=2pxy^2=-2pxx^2=2pyx^2=-2py。
4.对于平面内任意一点C，过点C分别向X轴、Y轴作垂线，垂足在X轴、Y轴上的.对应点a，b分别叫做点C的横坐标、纵坐标，有序实数对（a，b）叫做点C的坐标。
5.公因式：一个多项式每项都含有的公共的因式，叫做这个多项式各项的公因式。

本文关键词：抛物线的基本概念和性质，抛物线的讲解，抛物线的基本知识点有哪些高中，抛物线的相关知识，抛物线的相关知识点公式。这就是关于《抛物线的基本知识点，抛物线的基本知识点有哪些（高中数学椭圆、双曲线、抛物线的重点知识归纳和常用结论汇总）》的所有内容，希望对您能有所帮助！更多的知识请继续关注《犇涌向乾》百科知识网站：http://www.029ztxx.com！