关于【折线统计图的特点】，折线统计图的特点和作用，今天向乾小编给您分享一下，如果对您有所帮助别忘了关注本站哦。

1、折线统计图的特点

折线统计图的特点：易于显示数据变化的趋势和变化的幅度，可以直观地反映变化和组间的差异。折线统计图用折线的起伏表示数据的增减变化情况。不仅可以表示数量的多少，而且可以反映数据的增减变化情况。折线统计图可以用来作股市的跌涨和统计气温或其他表示趋势的资料。

折线统计图主要用途：表示现象间的对比关系；揭露总体结构；检查计划的执行情况；揭示现象间的依存关系，反映总体单位的分配情况；说明现象在空间上的分布情况。

折线统计图一般采用直角坐标系．横坐标用来表示事物的组别或自变量x，纵坐标常用来表示事物出现的次数或因变量y；或采用角度坐标（如圆形图）、地理坐标（如地形图）等。

折线图可分为动态折线图、依存关系折线图和次数分布折线图。人们常用折线图来描绘统计事项总体指标的动态、研究对象间的依存关系以及总体中各部分的分配情况等。

2、四年级数学下册全册知识要点（附易错题解析）

四年级数学下册各单元知识要点

第一单元《四则运算》

知识点1：没有括号的同级运算。

在没有括号的算式里，如果只有加、减法或乘、除法运算，要按照从左到右的顺序计算。

计算加减混合运算，有时为了计算简便，可以适当调整算式中运算的顺序，要把题中的某数带着数前的运算符号“搬家”。

213+48－13

=213－13+48 【学生容易写成

=200+48 213+13－48】

=248

72×36÷8

=72÷8×36【学生容易写成

=9×36 72×8÷36 】

=324

易错题： 15÷5×3 25×3÷25×3

=15÷15 =75÷75

=1 =1

这两道题是没有掌握好同级运算的顺序，认为怎样好算就怎样算。

知识点2：没有括号的四则混合运算。

在没有括号的算式里，有乘、除法和加、减法，要先算乘、除法，后算加、减法。

易错题：75+25÷5 134－34÷34+66

=100÷5 =100÷100

=20 =1

这两道题还是没有掌握好四则混合运算的顺序，算式中有乘除法和加减法，要先算乘除法，后算加减法。学生认为怎样好算怎样算。

知识点3：带括号的四则混合运算。

含有小括号的混合运算，要先算括号里面的，再算括号外面的。

知识点4：运用混合运算解决问题。

分析、弄清题中的条件与问题的关系，其实就是解决应用题常见的一种方法——分析法。它是从应用题要求的未知数入手，根据数量关系，找出解答最后结果所需条件，把其中的一个或两个未知条件作为要解的问题，然后找出解决这一个或两个问题所需要的条件，这样逐步逆推，直到所找的条件在应用题中都是已知的为止。

易错题：张师傅要生产600个零件，已经生产了120个，剩下的要10天完成，平均每天生产多少个？

600－120÷10

=480÷10 （学生知道应先算减法，但总忘加括号）

=48（个）

解题时要弄清数量之间的关系与先后顺序，如果要先算第一级运算，一定要在第一级运算上加上小括号。

第二单元《位置与方向》

知识点1：确定物体位置的条件。

方向和距离，两个条件缺一不可。

知识点2：在平面图上标出物体位置的方法。

先确定方向，在确定距离，最后画出物体具体位置，并标明名称。确定方向时选择与物体所在离得较近（夹角较小）的方位；距离必须以选定的单位长度为基准来确定。

巧计：物体位置要想找，方向、距离缺不了。

方向确定在找角，一般选小是首要。

距离大小有参数，下方标注不可少。

易错题：①如图，A点是学校的教学楼，B点是体育馆，则体育馆在教学楼的北偏西30⁰方向上。

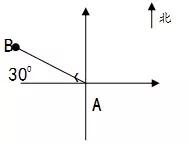
此题错在对教学楼的具体方向的叙述不清楚。30⁰角是由正西方向偏向北得到的，所以叙述时应先说西方，再说北方。

正确答案为：体育馆在教学楼的西偏北30⁰方向上。

在叙述物体的方向时，一般先说与物体所在方向离得较近（夹角较小）的方位。

②小明家在小东家南偏西40⁰方向500米处，画平面图表示小明家的位置如下：

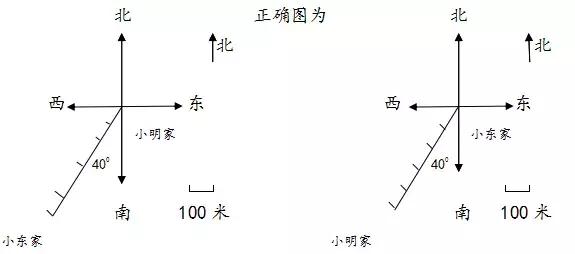
此题错误有两处：一是观测点确定不对，应以小东家为观测点画方向标；二是单位长度不统一，小明家到小东家的距离应以图标为准，画出5个等长的 。

技巧：画平面图时，首先要确定好观测点，其次确定被观测物体的方向，最后以选定的单位长度为基准来确定距离。

知识点3：物体位置的相对性。

叙述物体的位置时，要考虑物体位置的相对性，如何叙述物体的位置与观察点有关，观测点不同，物体位置的叙述就不同。

易错题：①甲地在乙地的东偏北30⁰方向900米处，也可以说乙地在甲地的西偏南60⁰方向900米处。

此题错在对位置的相对性理解不好，对角的度量知识掌握不扎实。

画图理解更直观：

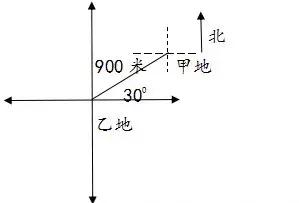
正确解答为甲地在乙地的东偏北30⁰方向900米处，也可以说乙地在甲地的西偏南30⁰方向900米处.

技巧：两地的位置具有相对性，以这两个不同地点为观测点描述对方所在地的方向时，方向正好相反（东→西，北→南，东偏北→西偏南）。

②画出活动中心与幼儿园的位置。

A活动中心在广场的西偏北20⁰方向50米处。

B幼儿园在活动中心的南偏东40⁰方向100米处。

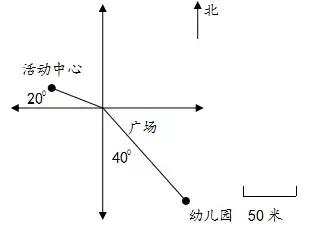
此题错在审题不认真。幼儿园的位置是相对于活动中心而说的，就应以活动中心为观测点建立方向标来确定幼儿园的位置。切忌确定物体的位置，观测点一定要找准。

知识点4：描述路线图的方法。

按行驶路线，先确定观测点及行走的方向和路程再描述。

第三单元《运算定律与简便运算》

知识点1：加法运算定律。（加法交换律和加法结合律）

加法交换律：两个加数交换位置，和不变。即a+b=b+a

加法结合律：先把前两个数相加，或者先把后两个数相加，和不变。即(a+b)+c= a+(b+c)

技巧：在一个加法算式中，当某些加数可凑成整十数或整百数时，运用加法交换律、加法结合律来改变运算顺序，可以使计算简便。

易错题：182+765+108

=182+108+765

=300+765 【计算失误，182与108的和不是300】

=1065

技巧：在进行加法简便计算时，有时两个数相加未必能凑成整百数，只能凑成整十数，因此要认真观察，准确计算。

24+127+476+573

=24+476+127+573 【（24+476）+（127+573）】

=500+700

=1200

此题错在没有真正理解加法的运算定律，运用加法结合律时要注意把结合的两个数用括号括起来。

加法运算定律的灵活运用：

计算256+249+251+246

=250+6+250－1+250+1+250－4

=250×4+（6－1+1－4）

=1000+2

=1002

技巧：当几个数相加，加数都比较接近某一个数时，可以把这个数作为基准数，看看有多少个这样的基准数，然后加上或减去比基准数多或少的数，求出结果。这种方法简称基准数加法。

知识点2：乘法运算定律。（乘法交换律、乘法结合律和乘法分配律）

乘法交换律：交换两个因数的位置，积不变。a×b=b×a

乘法结合律：先乘前两个数，或者先乘后两个数，积不变。

即(a×b)×c= a×(b×c)

乘法分配律：两个数的和与一个数相乘，可以把它们与这个数分别相乘，再相加。或两个数的差与一个数相乘，可以把它们与这个数分别相乘，再把所得的积相减。

即(a±b)×c= a×c±b×c或a×（b±c）= a×b±a×c

（多个数的和或差与一个数相乘，可以把这些数分别与这个数相乘，再相加或相减。即(a±b±c)×m= a×m±b×m±c×m）

易错题： 50×(4×5)

=50×4+50×5【混淆了乘法结合律与乘法分配律】

=200+250

=450

技巧：只有运用运算定律能使运算简便时，才能运用运算定律，否则直接按四则混合运算顺序计算。乘法结合律与乘法分配律的最大区别是乘法分配律必须在乘、加或乘、减两种运算中进行。

76×101

=76×100+1【没有正确理解乘法分配律，76×101可以想成=7600+1 是101个76，也就是100个76与1个76的和。】

=7601

15×21+15×78+15

=15×（21+78）+15【虽然计算结果正确，但在简算过程中没

=15×99+15

有把第三项“15”看成“15×1”参与=1485+15 到计算中，而导致计算不是最简便。】

=1500

技巧：正确理解乘法分配律是运用好乘法分配律的前提。运用简便算法计算时，一定要仔细观看算式结构及数的特点，有时需将一个数转化成两数乘积的形式再进行简便计算。

乘法运算定律的灵活运用：

计算25×32×125

=25×（4×8）×125

=（25×4）×（8×125）

=100×1000

=100000

技巧：在乘法计算中，也有“凑整”的计算。如：2×5=10,25×4=100,125×8=1000.因此计算连乘算式时，当有的因数不具备“凑整”条件时，可以运用分解的方法，把一个因数分解为两个因数相乘的形式，是其中的因数与其他数的乘积“凑整”，这样会使计算更简便。

知识点3：连减的简便计算。

减法性质：

①一个数连续减去两个减数，可以用这个数去这两个减数的和，即a－b－c=a－(b+c)。

②在连减运算中，任意交换减数的位置，差不变。

即a－b－c= a－c－b。

注意：括号前面是加号，去掉括号，原括号内运算符号不改变；加号后面添括号，括号里面原运算符号不变号；括号前面是减号，去掉括号，原括号内运算符号要变号；即a－（b－c）=a－b+c；减号后面添括号，括号里面原运算符号要变号即a－b+c= a－（b－c）。

易错题：596－48+52

=596－100 【此题错在审题不认真，只看数据能否凑整，

=496 而忽略了算式的整体性。】

技巧：加、减混合运算中，要想交换数的位置，一定要连同前面的运算符号一同交换；加括号时，如果括号前面是加号，括号里面不变号，如果括号前面是减号，括号里面要变号。

762－598

=762－600－2 【没有真理解“凑整”的意义，把598看成600 =162－2 时，已经多减去一个2，就应加上一个2.】

=160

技巧：在加法或减法计算中，当某个数接近整十、整百、整千时，可以把这个数当成整十、整百、整千的数进行加、减，对于原数与整十、整百、整千相差的数，要根据“多加要减去，少加还要加，多减要加上，少减还要减”的原则进行处理。

知识点4：连除的简便计算。

除法的性质：

①一个数连续除以两个数，可以用这个数除以两个除数的积，即a÷b÷c=a÷(b×c)。

②一个数连续除以几个数，任意交换除数的位置，商不变，即a÷b÷c÷d=a÷c÷b÷d= a÷d÷b÷c。

在一个除加、除减的算式中，当除数相同时，可以运用a÷c±b÷c =(a±b)÷c使运算简便。

易错题：500÷25×4

=500÷100 【错在随便改变运算顺序，导致计算结果错误】

=5

技巧：当乘除混合运算中不具备简算因素时，应按照从左到右的顺序计算。

解题口诀：

一看：看数的特点；

二想：想运用什么运算定律；

三做：再进行计算；

四查：检查是否正确。

第四单元《小数的意义和性质》

知识点1：小数的意义和小数的计数单位。

小数的意义：分母是10、100、1000……的分数可以用小数表示。小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……每相邻两个计数单位间的进率是10.

易错题：

①小数都比1（整数）小。

此题错在对小数认识不够，小数点的左边可以是任意的整数。没有最大的小数，也没有最小的小数。

②0.35里面有5个0.01.

此题错在对小数的意义理解不到位，因为小数是分数的另一种表示形式，所以将小数变成分数，更容易理解其意义。

③最大的一位小数是0.9.

此题错在对一位小数的概念认识不清。所谓一位小数，是指小数部分是一位的小数，而整数部分可以是任意的数。比如：10.9、100.9、999.9……都是一位小数。没有最大的一位小数，最小的一位小数是0.1.

知识点2：小数的读写法。

小数的读法：先读整数部分，按整数的读法读；再度小数点，小数点读作“点”；最后读小数部分，依次读出小数部分每一位上的数字。

小数的写法：先写整数部分，按照整数的写法去写，如果整数部分是零，就直接写“0”；再在个位的右下角点上小数点；最后依次写出小数部分每一个数为上的数字。

注意：读数时要写中国小写数字（语文的字），写数时要写阿拉伯数字，读小数部分时，一定要注意所有的“0”都要一一读出。

知识点3：小数的性质和小数的大小比较。

小数的性质：小数的末尾添上“0”或去掉“0”，小数的大小不变。

小数大小比较方法：先比较整数部分，整数部分大的那个数就大；整数部分相同的，十分位上的数大的那个数就大；十分位上的数也相同的，百分位上的数大的那个数就大……

易错题：

①0.2和0.20大小相等，意义相同。

此题错在对小鼠的意义认识不清。0.2的计数单位是1／10，表示2个0.1，而0.20的计数单位是1／100，表示20个0.01，因此0.2和0.20表示的意义不同。小数的末尾添上“0”或去掉“0”，虽然不改变小数的大小，但计数单位却发生了变化。

②大于5且小于6的小数只有9个。

此题错在缩小了小数的取值范围。如果以1／10为计数单位，则5.1～5.9都是大于且小于6的一位小数；如果以1／100为计数单位，则5.01～5.99都是大于且小于6的两位小数；以此类推，如果没有小数数位的界定，大于5且小于6的小数应有无数个。切记两个整数间的小数有无数个。

知识点4：小数点移动引起小数大小变化的规律及应用。

小数点移动引起小数大小变化的规律：小数点向右移动一位，小数就扩大到原数的10倍；移动两位，小数就扩大到原数的100倍，移动三位，小数就扩大到原数的1000倍……反之，小数点向左移动一位，小数就缩小到原数的1／10；移动两位，小数就缩小到原数的1／100，移动三位，小数就缩小到原数的1／1000……

小数点移动引起小数大小变化的规律的应用：把一个数扩大到它的10倍、100倍、1000倍、……就是用这个数分别乘10、100、1000……

小数点就要相应的向右移动一位、两位、三位……把一个小数缩小到它的1／10、1／100、1／1000……就是把这个数分别除以10、100、1000……小数点就要相应的向左移动一位、两位、三位……

注意：小数点向右移动时，整数部分最高位前面的0必须去掉（0.3）；如果小数部分不够，要在右边添“0”补足数位。要数清移动的位数

知识点5：名数的改写。

注意：在改写60千克=( )吨时，不要写成0.6吨，应是0.06吨。还有面积单改写易错，如5平方米=（ ）平方分米，错写成50平方分米，进率是100. 应是500平方分米。

知识点6：求一个小数的近似数。

求小数近似数的方法：求小数近似数可以用“四舍五入法”。当保留整数时，表示精确到个位，应根据十分位上数字的大小来判断是否进位；保留一位小数时，表示精确到十分位，应根据百分位上数字的大小来判断是否进位；保留两位小数时，表示精确到百分位，应根据千分位上数字的大小来判断是否进位……

把不是整万或整亿的数改写成用“万”或“亿”作单位的数的方法：

先确定万位或亿位，然后在万位或亿位的右下角点上小数点，最后在小数的后面加上“万”字或“亿”字，如果小数的末尾有0要去掉，改写后还可以根据要求保留小数。

注意：保留几位小数，只要看保留小数位数的下一位，后面无论有多少位数，都不用考虑。求近似数时，一定要用“≈”连接；改写成用“万”或“亿”作单位的数时，位数不够，在前面添“0”补足。

第五单元《三角形》

知识点1：三角形的定义与特性。

三角形的定义：由三条线段围成的图形（每相邻两条线段的端点相连）角做三角形。从三角形的一个顶点到它的对边作一条垂线，顶点和垂足之间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形具有稳定性。

易错题：直角三角形只有一条高。

此题错在没有认识到直角三角形的两条直角边也是直角三角形的高。任意一个三角形都有三条高。

还有画高时，一定要保证垂线和底边相交所成的角是直角。

知识点2：三角形的三遍的关系。

三角形任意两边的和大于第三边。

判断三条线段是否能围成三角形，只要把最短的两条边相加与最长变比较即可。如果最短的两条边之和大于第三边，也就证明任意两条边之和大于第三边。

知识点3：三角形的分类。

三角形按角分为：锐角三角形、直角三角形和钝角三角形。因为在一个三角形中至少有两个锐角，所以可以根据最大的角判断三角形的类型。最大的角是哪类角，它就属于那类三角形。

三角形按边分为：不等边三角形和等腰三角形，等腰三角形包括等边三角形。

易错题：等腰三角形一定是锐角三角形。

此题错在对等腰三角形概念理解模糊。两边相等的三角形就是等腰三角形，它与角的大小无关。在直角三角形和钝角三角形中，如果有两条边相等，也可以称其为等腰三角形。等腰三角形可以是锐角三角形、直角三角形和钝角三角形。

知识点4：三角形的内角和。

知道三角形内角和是180⁰.并会根据要求求其它角。

易错题：判断一个三角形中最多有两个直角。（√）

此题错在不会应用三角形内角和180⁰来分析问题。一个三角形中最多有一个直角。

知识点5：图形的拼组。

任意两个相同的三角形都可以拼成一个平行四边形；两个相同的直角三角形可以拼成一个长方形或平行四边形；两个相同的等腰直角三角形可以拼成一个正方形或平行四边形；三个相同的三角形可以拼成梯形。

易错题：①只有完全相同的两个三角形才可以拼成四边形。

此题错在不清楚三角形拼摆四边形的条件。当两个三角形有一条边相等时，这两个三角形就可以拼成四边形。而只有完全相同的两个三角形才可以拼成一个平行四边形。

②两个相同的直角三角形一定能拼成一个正方形。

此题错在结论过于绝对化，当直角三角形的两条直角边不相等时，拼成的四边形只能是长方形。

两个相同的直角三角形（非等腰）可以一拼成一个长方形。

第六单元《小数的加法和减法》

知识点1：小数的加、减法。

笔算小数加、减法要注意：

1.计算小数加、减法时，要注意小数点对齐，也就是把相同数位对齐。

2.从低位算起，按整数加、法进行计算，得数对齐小数点的位置，点上小数点。

3.得数（指小数）的末尾有0，一般要去掉。

易错题：16.5－13.81=2.71

16.5 【错在减数百分位上的1 不应落下来，而应－13.81 把被减数16.5看成16.50再计算。】2.71

技巧：在笔算小数减法时，当小数位数不同时，可以根据小数的性质在小数末尾添上0，使两个小数数位相同后再相减。还要看清运算符号后再计算。

知识点2：小数的四则混合运算。

小数加减混合运算的运算顺序同整数加减混合运算顺序相同。

易错题：35.65－（18.65+4.15）

=35.65－18.65+4.15【去括号没有改变括号内的运算符号】

=17+4.15

=21.15

技巧：此题可用减法性质1的逆运算来解决，还可以运用整数运算中去括号的方法解决。

27.24+18.6－20.3

=29.1－20.3 【错在相同数位没对齐，百分位上的4要落下来，十分位上的2应与6相加。】

=8.8

知识点3：小数加减法的简便运算。

整数的运算定律在小数运算中同样适用。

易错题：①5.84+4.16－5.84+4.16

=（5.84+4.16）－（5.84+4.16）

=10－10 【审题不认真，只看数据的特点，却忽略了数 与数之间的关系及每个数前面的运算符号】

=0

技巧：小数加减混合运算中，要想交换数的位置，一定要连同数前面的运算符号一同交换。

②15.46－5.7+4.3

=15.46－(5.7+4.3)

=15.46－10 【此题只考虑数据能否凑整，而忽略了简算是否可行。】

=5.46

技巧：简算时如果需要加括号，一定要注意变号规则：如果在加号后加括号，括号里面不变号；如果在减号后加括号，括号里面要变号。

第七单元《统计》

知识点1：折线统计图的画法及折线统计图的特点。

折线统计图的特点：既可以反映数量的多少，又能反映数量的增减变化。在实际问题中，如果需要了解数量增减变化，选用折线统计图比较合适。

画折线统计图的步骤：①描点；②连点成线段；③标明数据。描点时应注意先找准横轴上的点，在找准纵轴上相对应的点，过两点画横轴、纵轴的垂线，两条垂线的交点便是所要描的点。

注意：①描点时一定要关注所描点的位置与纵轴上的数据是否对应。②如果所选统计的一组数据比较大时，可选择最小的数据为基础数，0至基础数这一段用折线表示。③绘制时要根据实际问题中的数据特点来确定绘制什么样的统计图。一般情况下，条形统计图可以表示数据的多少，折线统计图不仅表示数据的多少，还表示数据增减变化的情况。

知识点2：运用折线统计图进行数据的分析和数据的预测。

可以根据统计图发现问题、解决问题并进行简单的预测。

第八单元《数学广角》

知识点1：关于一条线段且两端植树的问题：指数的棵树=间隔数+1。

知识点2：关于一条线段且两端不植树的问题：指数的棵树=间隔数－1。

知识点3：关于一个封闭图形的植树问题：指数的棵树=间隔数。

封闭图形的周长=间隔数×株树。较复杂的应用题从问题入手进行分析更有助于问题的解决。

本文关键词：条形统计图的特点，条形统计图和折线统计图的特点，条形统计图扇形统计图折线统计图的特点，扇形条形折线统计图的特点，扇形统计图的特点。这就是关于《折线统计图的特点，折线统计图的特点和作用（四年级数学下册全册知识要点）》的所有内容，希望对您能有所帮助！更多的知识请继续关注《犇涌向乾》百科知识网站：http://www.029ztxx.com！